https://programmers.co.kr/learn/courses/30/lessons/67259
코딩테스트 연습 - 경주로 건설
[[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0],[0,0,0,0,0,1,0,0],[0,0,0,0,1,0,0,0],[0,0,0,1,0,0,0,1],[0,0,1,0,0,0,1,0],[0,1,0,0,0,1,0,0],[1,0,0,0,0,0,0,0]] 3800 [[0,0,1,0],[0,0,0,0],[0,1,0,1],[1,0,0,0]] 2100 [[0,0,0,0,0,0],[0,1,1,1,1,0],[0,0,1,0,0,0],[1,0,0,1,0,1],[
programmers.co.kr
문제 설명

건설회사의 설계사인 죠르디는 고객사로부터 자동차 경주로 건설에 필요한 견적을 의뢰받았습니다.
제공된 경주로 설계 도면에 따르면 경주로 부지는 N x N 크기의 정사각형 격자 형태이며 각 격자는 1 x 1 크기입니다.
설계 도면에는 각 격자의 칸은 0 또는 1 로 채워져 있으며, 0은 칸이 비어 있음을 1은 해당 칸이 벽으로 채워져 있음을 나타냅니다.
경주로의 출발점은 (0, 0) 칸(좌측 상단)이며, 도착점은 (N-1, N-1) 칸(우측 하단)입니다. 죠르디는 출발점인 (0, 0) 칸에서 출발한 자동차가 도착점인 (N-1, N-1) 칸까지 무사히 도달할 수 있게 중간에 끊기지 않도록 경주로를 건설해야 합니다.
경주로는 상, 하, 좌, 우로 인접한 두 빈 칸을 연결하여 건설할 수 있으며, 벽이 있는 칸에는 경주로를 건설할 수 없습니다.
이때, 인접한 두 빈 칸을 상하 또는 좌우로 연결한 경주로를 직선 도로 라고 합니다.
또한 두 직선 도로가 서로 직각으로 만나는 지점을 코너 라고 부릅니다.
건설 비용을 계산해 보니 직선 도로 하나를 만들 때는 100원이 소요되며, 코너를 하나 만들 때는 500원이 추가로 듭니다.
죠르디는 견적서 작성을 위해 경주로를 건설하는 데 필요한 최소 비용을 계산해야 합니다.
예를 들어, 아래 그림은 직선 도로 6개와 코너 4개로 구성된 임의의 경주로 예시이며, 건설 비용은 6 x 100 + 4 x 500 = 2600원 입니다.
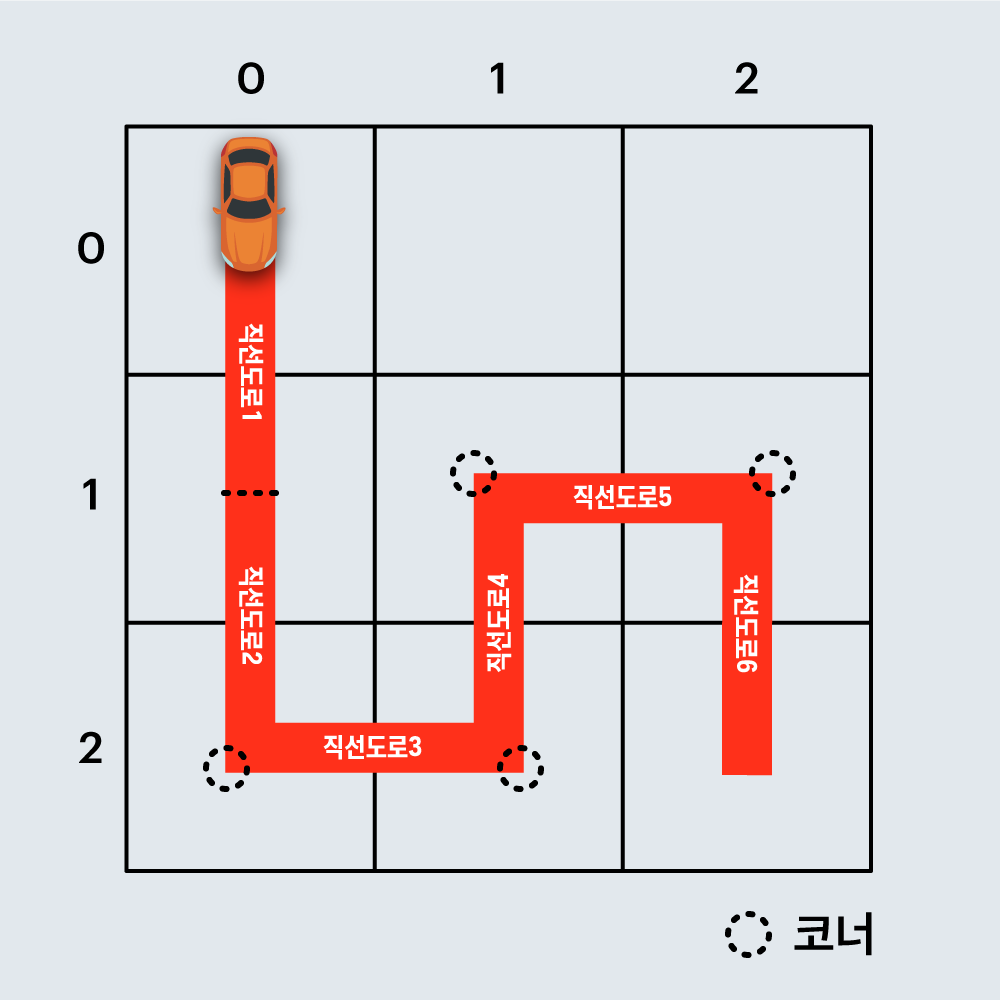
또 다른 예로, 아래 그림은 직선 도로 4개와 코너 1개로 구성된 경주로이며, 건설 비용은 4 x 100 + 1 x 500 = 900원 입니다.
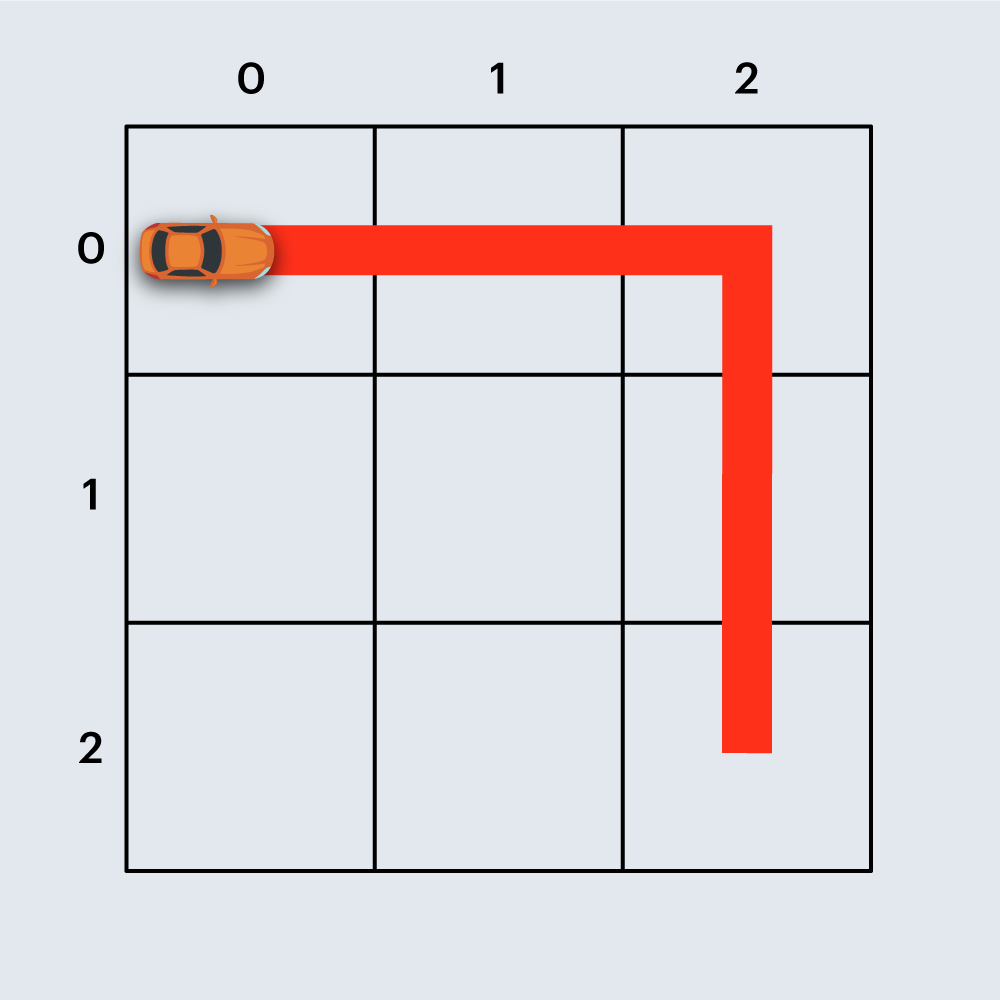
도면의 상태(0은 비어 있음, 1은 벽)을 나타내는 2차원 배열 board가 매개변수로 주어질 때, 경주로를 건설하는데 필요한 최소 비용을 return 하도록 solution 함수를 완성해주세요.
[제한사항]
- board는 2차원 정사각 배열로 배열의 크기는 3 이상 25 이하입니다.
- board 배열의 각 원소의 값은 0 또는 1 입니다.
- 도면의 가장 왼쪽 상단 좌표는 (0, 0)이며, 가장 우측 하단 좌표는 (N-1, N-1) 입니다.
- 원소의 값 0은 칸이 비어 있어 도로 연결이 가능함을 1은 칸이 벽으로 채워져 있어 도로 연결이 불가능함을 나타냅니다.
- board는 항상 출발점에서 도착점까지 경주로를 건설할 수 있는 형태로 주어집니다.
- 출발점과 도착점 칸의 원소의 값은 항상 0으로 주어집니다.
입출력 예
| board | result |
| [[0,0,0],[0,0,0],[0,0,0]] | 900 |
| [[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0],[0,0,0,0,0,1,0,0],[0,0,0,0,1,0,0,0],[0,0,0,1,0,0,0,1],[0,0,1,0,0,0,1,0],[0,1,0,0,0,1,0,0],[1,0,0,0,0,0,0,0]] | 3800 |
| [[0,0,1,0],[0,0,0,0],[0,1,0,1],[1,0,0,0]] | 2100 |
| [[0,0,0,0,0,0],[0,1,1,1,1,0],[0,0,1,0,0,0],[1,0,0,1,0,1],[0,1,0,0,0,1],[0,0,0,0,0,0]] | 3200 |
입출력 예에 대한 설명
입출력 예 #1
본문의 예시와 같습니다.
입출력 예 #2

위와 같이 경주로를 건설하면 직선 도로 18개, 코너 4개로 총 3800원이 듭니다.
입출력 예 #3

위와 같이 경주로를 건설하면 직선 도로 6개, 코너 3개로 총 2100원이 듭니다.
입출력 예 #4

붉은색 경로와 같이 경주로를 건설하면 직선 도로 12개, 코너 4개로 총 3200원이 듭니다.
만약, 파란색 경로와 같이 경주로를 건설한다면 직선 도로 10개, 코너 5개로 총 3500원이 들며, 더 많은 비용이 듭니다.
풀이
최단 거리를 구하는 문제이며, 일반적으로 BFS를 이용하면 답을 구할 수 있습니다. 문제라면 회전에 대한 가중치가 포함되어 있다는 점이겠네요. 직진 시에는 직선 도로만 추가되므로 +100, 커브 시에는 직선 도로 + 코너가 추가되므로 +600을 해줍니다. x, y 좌표 이외에도 직진인지 커브인지 평가하기 위한 정보가 필요하겠네요.
또한, 예시 3. 4에서 볼 수 있듯이 최소 비용을 찾기 위해 이미 탐색한 경로를 다시 확인해야 하는 경우가 존재합니다. 일반적인 BFS의 경우 isVisit에 T/F 값을 지정하여 탐색 여부를 결정한다면, 위 문제에서는 isVisit에 Cost를 저장하고, 다시 방문했을 때의 Cost가 더 작다면 방문을 허용하는 식으로 작업했습니다.
최초에는 어느 방향으로 진행하던 코너가 생기지 않는다는 점에 주의합니다.
def solution(board):
n = len(board)
opened = [(0,0,-1,0)] # y, x, direction, cost
closed = [[-1 for _ in range(n)] for _ in range(n)]
answer = -1
while opened:
y, x, d, c = opened.pop(0)
if (y, x) == (n-1, n-1) and (answer == -1 or answer > c):
answer = c
neighbors = [(y, x-1), (y, x+1), (y-1, x), (y+1, x)]
for direction, (ny, nx) in enumerate(neighbors):
# boundary
if ny <= -1 or ny >= n or nx <= -1 or nx >= n:
continue
# wall
if board[ny][nx]:
continue
# visited and cheaper
cost = c + (100 if d == direction or d == -1 else 600)
if closed[ny][nx] != -1 and closed[ny][nx] < cost:
continue
opened.append((ny, nx, direction, cost))
closed[ny][nx] = cost
return answer'알고리즘' 카테고리의 다른 글
| [프로그래머스] 순위 #파이썬 #그래프 #Floyd-Warshall #Level3 (2) | 2021.05.24 |
|---|---|
| [프로그래머스] 숫자 게임 #파이썬 #정렬 #Greedy [Summer/Winter Coding(~2018)] (0) | 2021.05.22 |
| [프로그래머스] 징검다리 건너기 #python3 #이진탐색 binary search [2019 카카오 개발자 겨울 인턴십] (0) | 2021.05.21 |
| [프로그래머스] 기지국 설치 #파이썬 #Python [Summer/Winter Coding(~2018)] (1) | 2021.05.21 |
| [HackerRank] Fraudulent Activity Notifications #이진탐색 #이분탐색 #바이너리서치 #bisect #sort (0) | 2021.05.20 |


