Empty Cell
네 개의 공간이 있고, 각각의 공간에 파티클이 존재할 확률이 모두 같을 때(=uniform), 파티클을 N개 생성해서 칸 A에 파티클이 존재하지 않을 확률을 구하세요.
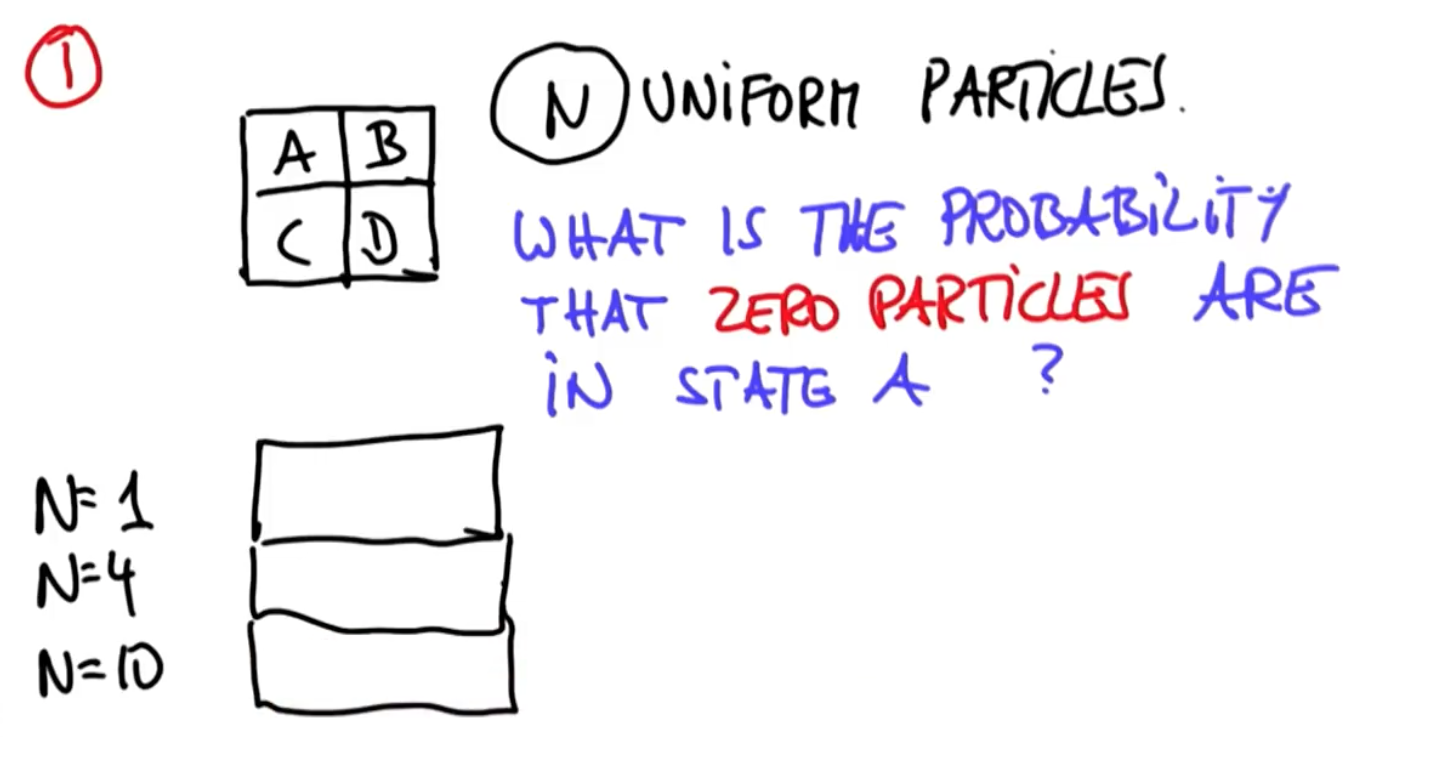
답은 다음과 같습니다. 칸 A에 파티클이 존재하지 않을 확률은 0.75, 이를 N 번 반복한다고 생각하면, 칸 A에 파티클이 존재하지 않을 확률은 0.75 ** N이 됩니다.

Motion Question
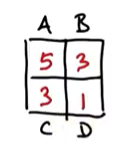
아까와 같은 공간에서 다음과 같은 상황이라고 해봅시다. A에 5개의 파티클, B에 3개, C에 3개, D에 1개의 파티클이 존재합니다.
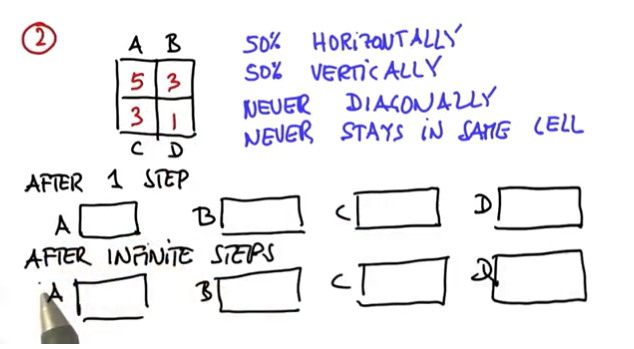
로봇이 움직인다고 합시다. 측정은 하지 않고요. 로봇은 50% 확률로 가로로 움직이고, 50% 확률로 세로로 움직입니다. 대각선으로 움직이거나, 제자리에 있는 경우는 없습니다.

1번 이동 후 파티클의 상황은 어떻게 달라질까요? 계속해서 움직이면요?
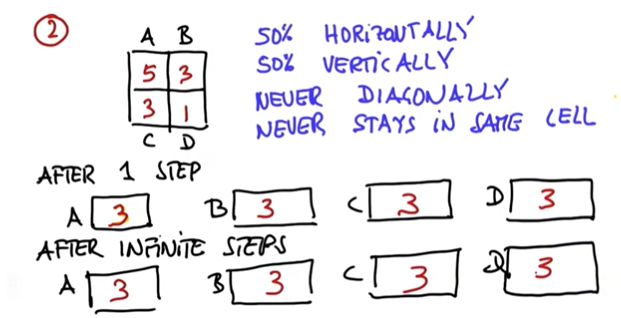
이전 시간에 우리는 이동으로 통해 컨볼루션 된다고 이야기 했습니다. 확률과 파티클의 곱을 모두 더하면 업데이트 된 값을 확인할 수 있습니다.

1번 이동 후 A가 되는 경우는 B에서 오는 경우와 C에서 오는 경우입니다. 해당 값을 모두 더하면 0.5 * 3 + 0.5 * 3 = 3입니다. 1번 이동 후 B가 되는 경우는 A에서 오는 경우와 D에서 오는 경우입니다. 해당 값을 모두 더하면 0.5 * 5 + 0.5 * 1 = 3입니다.
모든 공간의 파티클 개수가 같아졌으니 이후 이동 또한 3으로 수렴합니다.
Single Particle
이번에는 직관을 시험해봅시다. 파티클이 단 하나만 존재한다고 했을 때 해당 파티클 필터는 잘 작동할까요? 아니면 로봇의 측정이나 이동을 무시할까요? 실패할 가능성이 있나요? 올바른 걸 모두 고르세요.

정답은 아래와 같습니다. 파티클이 하나이면, 가중치에 따라 파티클을 재생성할 때 항상 동일한 파티클이 재생성 됩니다. 로봇이 이동하면 파티클도 이동하긴 하겠지만 언제나 로봇과 일정한 오프셋을 유지하겠지요. 이러한 파티클 필터로는 로봇 위치 추정을 시행할 수 없습니다.

Circular Motion
자동차를 생각해봅시다. 두 개의 방향 조절 바퀴와 두 개의 직진 바퀴가 있습니다. 로봇의 위치 x, y는 두 직진 바퀴의 중점, 방향을 나타내는 세타가 있습니다.
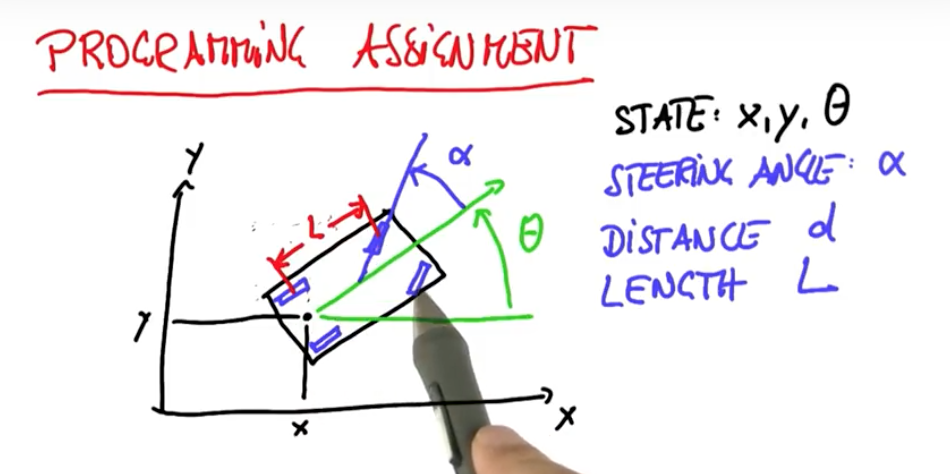
핸들을 꺾은 각도는 알파, 이동 거리는 d, 로봇의 길이는 앞뒤 바퀴 사이의 거리 L로 나타냅니다.
이렇게 앞 바퀴만 회전할 수 있는 자동차를 자전거 모델이라고 합니다. 두 바퀴는 평행하게 움직이니 한 쪽만 따로 떼어놓고 생각하겠습니다.
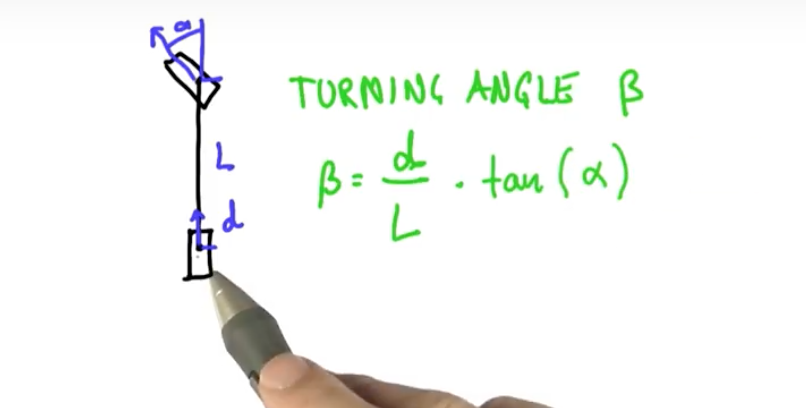
로봇이 움직인 거리 d와 핸들을 꺾은 각도 알파와 로봇 길이 L이 주어졌을 때, 로봇이 실제 회전하게 되는 각도 베타는 다음과 같습니다.
b = d / L * tan(a)
R = d / b
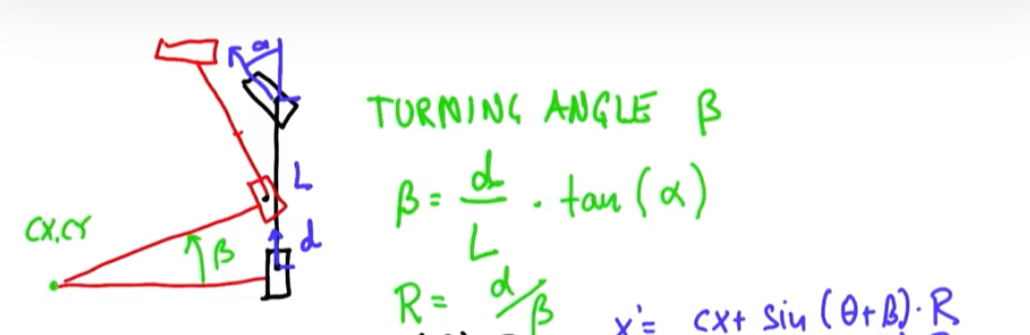
알파가 일정하면 로봇은 일정한 호를 그리며 이동합니다. 이때 중심점을 cx, cy라고 하면, cx, cy를 구하는 공식은 다음과 같습니다. (알파 = a, 베타 = b, 세타 = t)
cx = x - sin(t) * R
cy = y + cos(t) * R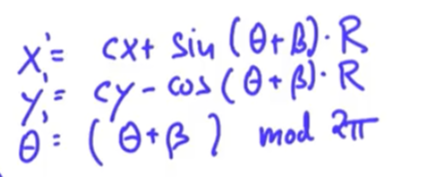
이를 토대로 x, y의 위치를 알아낼 수도 있습니다. 위치는 다음과 같이 업데이트 됩니다.
t' = (t + b) mod (2 * pi)
x' = cx + sin(t + b) * R = cx + sin(t') * R
y' = cy - cos(t + b) * R = cy - cos(t') * R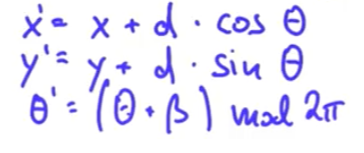
베타의 절댓값이 0.001보다 작을 때에는 zero division error 등을 막기 위해 다음 식을 사용합니다.
t' = (t + b) mod (2 * pi)
x' = x + d * cos(t)
y' = y + d * sin(t)이제 이런 공식을 가지고 move(self, motion) 함수를 완성해봅시다. motion 벡터는 핸들 각도 t와 거리 d로 이루어져 있습니다. 해당 함수는 이동 후 객체를 반환합니다. 코드 템플릿은 다음과 같습니다.
from math import *
import random
# --------
#
# the "world" has 4 landmarks.
# the robot's initial coordinates are somewhere in the square
# represented by the landmarks.
#
# NOTE: Landmark coordinates are given in (y, x) form and NOT
# in the traditional (x, y) format!
landmarks = [[0.0, 100.0], [0.0, 0.0], [100.0, 0.0], [100.0, 100.0]] # position of 4 landmarks
world_size = 100.0 # world is NOT cyclic. Robot is allowed to travel "out of bounds"
max_steering_angle = pi/4 # You don't need to use this value, but it is good to keep in mind the limitations of a real car.
# ------------------------------------------------
#
# this is the robot class
#
class robot:
# --------
# init:
# creates robot and initializes location/orientation
#
def __init__(self, length = 10.0):
self.x = random.random() * world_size # initial x position
self.y = random.random() * world_size # initial y position
self.orientation = random.random() * 2.0 * pi # initial orientation
self.length = length # length of robot
self.bearing_noise = 0.0 # initialize bearing noise to zero
self.steering_noise = 0.0 # initialize steering noise to zero
self.distance_noise = 0.0 # initialize distance noise to zero
def __repr__(self):
return '[x=%.6s y=%.6s orient=%.6s]' % (str(self.x), str(self.y), str(self.orientation))
# --------
# set:
# sets a robot coordinate
#
def set(self, new_x, new_y, new_orientation):
if new_orientation < 0 or new_orientation >= 2 * pi:
raise ValueError, 'Orientation must be in [0..2pi]'
self.x = float(new_x)
self.y = float(new_y)
self.orientation = float(new_orientation)
# --------
# set_noise:
# sets the noise parameters
#
def set_noise(self, new_b_noise, new_s_noise, new_d_noise):
# makes it possible to change the noise parameters
# this is often useful in particle filters
self.bearing_noise = float(new_b_noise)
self.steering_noise = float(new_s_noise)
self.distance_noise = float(new_d_noise)
############# ONLY ADD/MODIFY CODE BELOW HERE ###################
# --------
# move:
# move along a section of a circular path according to motion
#
def move(self, motion):
return result원래 설정되어 있던 length와 noise 값을 이어받습니다. steering과 distance에도 noise를 적용합니다. 이후로는 위 공식과 같습니다.
def move(self, motion, tolerance=0.001):
# alpha, d
steering, distance = motion
steering = random.gauss(steering, self.steering_noise)
distance = random.gauss(distance, self.distance_noise)
# L
res = robot(self.length)
res.set_noise(self.bearing_noise, self.steering_noise, self.distance_noise)
# beta
turn = distance / res.length * tan(steering)
# theta'
orientation = (self.orientation + turn) % (2.0 * pi)
if abs(turn) < tolerance:
x = self.x + distance * cos(self.orientation)
y = self.y + distance * sin(self.orientation)
else:
radius = distance / turn
cx = self.x - sin(self.orientation) * radius
cy = self.y + cos(self.orientation) * radius
x = cx + sin(orientation) * radius
y = cy - cos(orientation) * radius
res.set(x, y, orientation)
return resSensing
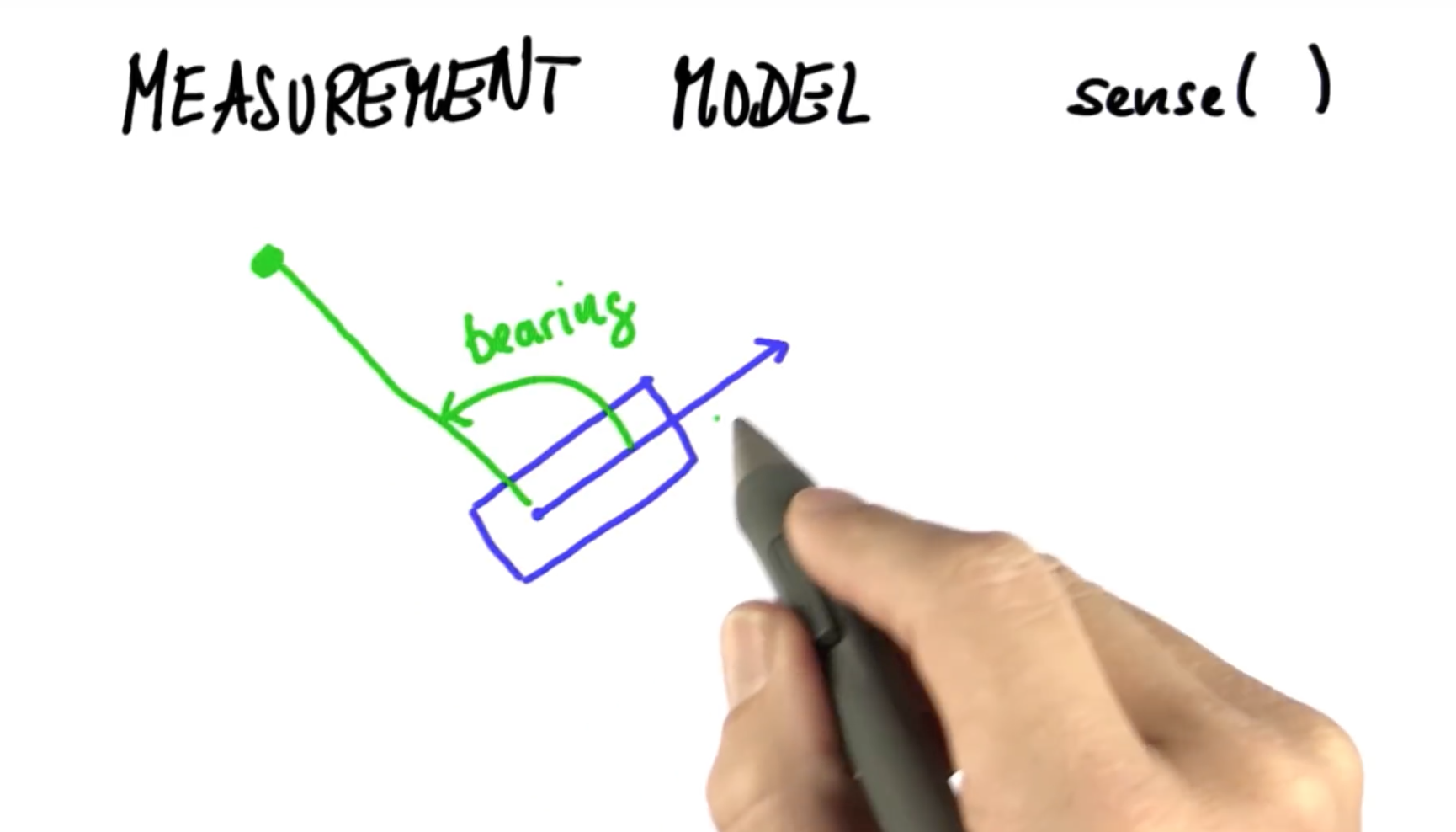
여기 자동차와 랜드마크가 있습니다. 자동차의 x,y와 랜드마크를 이은 선분과 오리엔테이션 벡터가 이루는 각도를 bearing이라고 합니다.
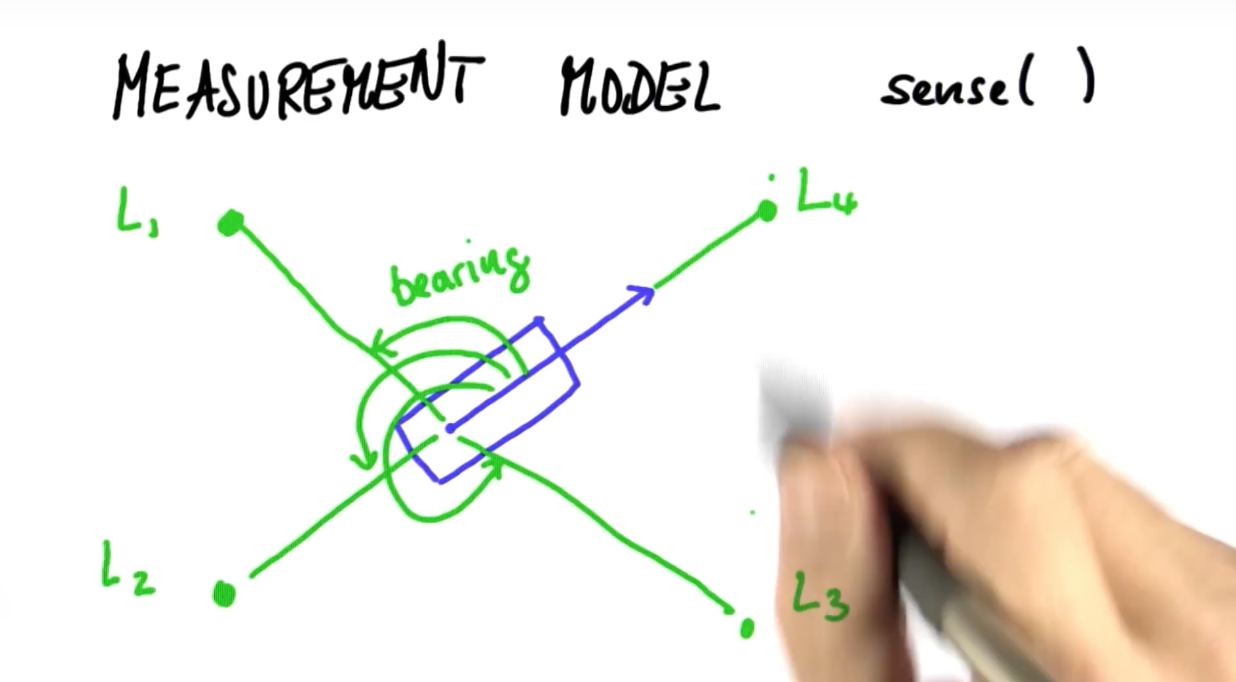
구분 가능한 랜드마크가 4개 있다면, 4개의 베어링을 측정할 수 있습니다.
atan2(dy, dx) 함수를 통해 글로벌 각도를 구할 수 있으며, 로봇의 오리엔테이션(=theta)을 빼주어 로컬 각도(=bearing)를 구할 수 있습니다.
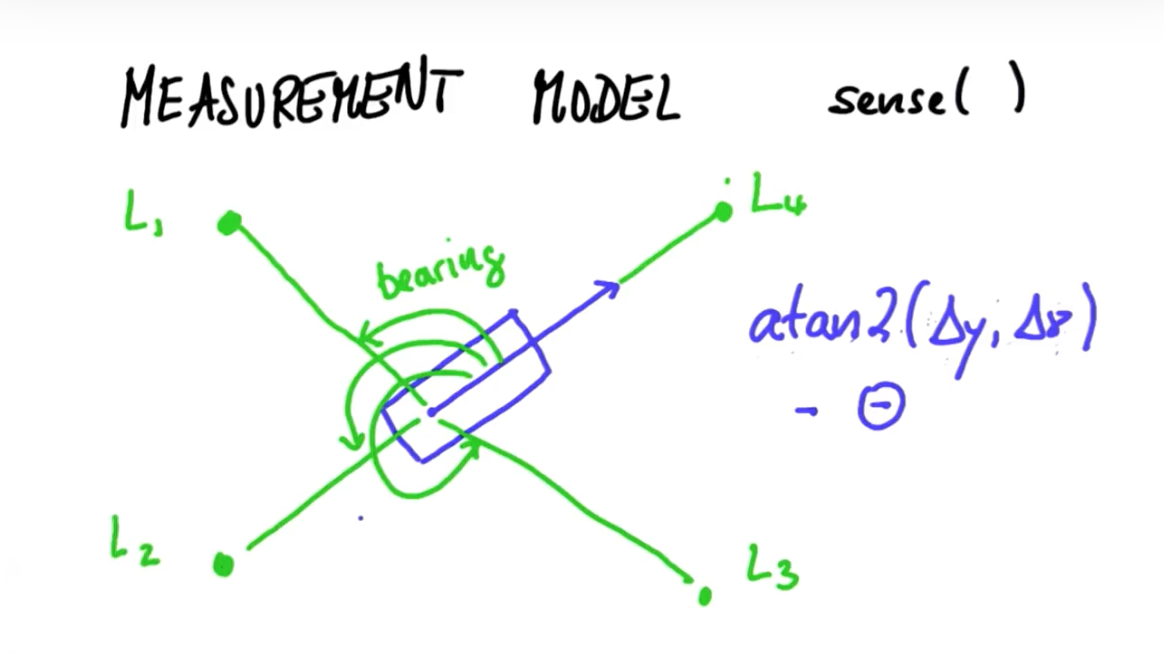
그렇다면 bearing을 직접 구해볼까요? 템플릿 코드의 sense()를 구현해봅시다. sense는 self만을 인풋으로 받고, 네 개의 bearing 리스트 Z를 반환합니다. 지금은 노이즈를 추가하지 않습니다. atan2를 통해 나온 값을 -pi ~ pi가 아닌, (거기에 orientation만큼 빼 범위를 알 수 없는 상태에서) 0 ~ 2pi 사이로 정규화 하기 위해 2pi로 나눈 나머지를 취합니다.
def sense(self):
Z = []
for y, x in landmarks:
dy = y - self.y
dx = x - self.x
bearing = atan2(dy, dx) - self.orientation
bearing %= (2.0 * pi)
Z.append(bearing)
return Z Final Quiz
이제 move와 sense에 노이즈를 집어넣어 봅시다. move에 steering_noise와 distance_noise를 추가하여 구현하세요.
sense에 더해주는 노이즈는 평균이 0, 분산이 bearing_noise입니다. 노이즈를 추가할지 결정하는 파라미터 add_noise를 추가하여 구현하세요. (디폴트 값은 1입니다.)
공식은 보더라도 코드는 보지 않도록 합니다. 그래야 실력이 느니까요.
# ... robot class ...
# --------
# move:
#
# copy your code from the previous exercise
# and modify it so that it simulates motion noise
# according to the noise parameters
# self.steering_noise
# self.distance_noise
def move(self, motion, tolerance=0.001):
result = robot(self.length)
result.set_noise(self.bearing_noise, self.steering_noise, self.distance_noise)
steering, distance = motion
steering = random.gauss(steering, self.steering_noise)
distance = random.gauss(distance, self.distance_noise)
turn = distance / result.length * tan(steering)
t_ = (self.orientation + turn) % (2.0 * pi)
if abs(turn) >= tolerance:
radius = distance / turn
cx = self.x - sin(self.orientation) * radius
cy = self.y + cos(self.orientation) * radius
x_ = cx + sin(t_) * radius
y_ = cy - cos(t_) * radius
else:
x_ = self.x + distance * cos(self.orientation)
y_ = self.y + distance * sin(self.orientation)
result.set(x_, y_, t_)
return result
# --------
# sense:
#
# copy your code from the previous exercise
# and modify it so that it simulates bearing noise
# according to
# self.bearing_noise
def sense(self, add_noise=1):
Z = []
for y, x in landmarks:
dy = y - self.y
dx = x - self.x
bearing = atan2(dy, dx) - self.orientation
if add_noise:
bearing += random.gauss(0, self.bearing_noise)
bearing %= 2.0 * pi
Z.append(bearing)
return Z


