48일차 - Particle Filter, 파티클 리샘플링, Resampling Wheel

파티클 리샘플링

생각했던 것보단 어렵겠지만, 시작해봅시다. 한 번 만들어 놓으면 이후에 어떤 파티클 필터 시스템에서도 사용할 수 있습니다.

여기 3개의 값(x, y, orientation)을 가지는 N 개의 파티클이 있습니다. 또한 N 개의 weights가 있죠. weights를 w1, ..., wN으로 표기하고, 이를 모두 합한 값을 W라고 표기하겠습니다.

weights를 노말라이즈 하는 과정은 이전에 Histogram Filter에서 했던 것과 비슷합니다. 노말라이즈 된 weights를 a1, ..., aN으로 표기하겠습니다.

a1 = w1 / W

고로 sum(a1, ..., aN) = 1이 됩니다.

이렇게 노말라이즈 된 weights를 사용하여 다시 파티클을 그립니다. a2가 크다면 여러 번 그리고, 값이 작으면 적게 그리는 식입니다.

Quiz

다음과 같이 5개의 파티클, weights가 있을 때 파티클이 다시 그려질 확률을 구하세요.

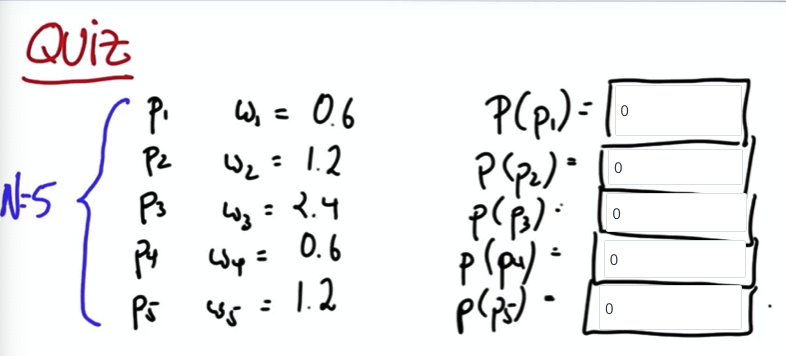
W = 6.0이므로 노말라이즈를 위해 모든 가중치를 6.0으로 나눠줍니다.

 

이렇게 구해진 가중치는 다음 번 파티클을 그릴 때 해당 파티클이 나타날 확률입니다. P1이 다시 그려지지 않는 경우가 있을까요?

확률이 0.1이니 당연히 있겠죠..

P3은요?? P3이 다시 나타나지 않을 확률이 있을까요? P1보다는 드물겠지만, 있을 수 있습니다. 그렇다면 P3이 등장하지 않을 확률은 정확히 얼마일까요?

P3이 나타날 확률은 0.4이므로 나타나지 않을 확률은 0.6입니다. 파티클 생성을 5번 반복하는 동안 P3이 나타나지 않을 확률은 0.6 ** 5 = 0.07776입니다.

Programming

이번에는 이전 코드에 이어 파티클을 리샘플링 하는 코드를 만들어봅시다. 템플릿 코드는 아래와 같습니다.

from math import *
import random

landmarks  = [[20.0, 20.0], [80.0, 80.0], [20.0, 80.0], [80.0, 20.0]]
world_size = 100.0

class robot:
    def __init__(self):
        self.x = random.random() * world_size
        self.y = random.random() * world_size
        self.orientation = random.random() * 2.0 * pi
        self.forward_noise = 0.0;
        self.turn_noise    = 0.0;
        self.sense_noise   = 0.0;

    def set(self, new_x, new_y, new_orientation):
        if new_x < 0 or new_x >= world_size:
            raise ValueError, 'X coordinate out of bound'
        if new_y < 0 or new_y >= world_size:
            raise ValueError, 'Y coordinate out of bound'
        if new_orientation < 0 or new_orientation >= 2 * pi:
            raise ValueError, 'Orientation must be in [0..2pi]'
        self.x = float(new_x)
        self.y = float(new_y)
        self.orientation = float(new_orientation)


    def set_noise(self, new_f_noise, new_t_noise, new_s_noise):
        # makes it possible to change the noise parameters
        # this is often useful in particle filters
        self.forward_noise = float(new_f_noise);
        self.turn_noise    = float(new_t_noise);
        self.sense_noise   = float(new_s_noise);


    def sense(self):
        Z = []
        for i in range(len(landmarks)):
            dist = sqrt((self.x - landmarks[i][0]) ** 2 + (self.y - landmarks[i][1]) ** 2)
            dist += random.gauss(0.0, self.sense_noise)
            Z.append(dist)
        return Z


    def move(self, turn, forward):
        if forward < 0:
            raise ValueError, 'Robot cant move backwards'         

        # turn, and add randomness to the turning command
        orientation = self.orientation + float(turn) + random.gauss(0.0, self.turn_noise)
        orientation %= 2 * pi

        # move, and add randomness to the motion command
        dist = float(forward) + random.gauss(0.0, self.forward_noise)
        x = self.x + (cos(orientation) * dist)
        y = self.y + (sin(orientation) * dist)
        x %= world_size    # cyclic truncate
        y %= world_size

        # set particle
        res = robot()
        res.set(x, y, orientation)
        res.set_noise(self.forward_noise, self.turn_noise, self.sense_noise)
        return res

    def Gaussian(self, mu, sigma, x):

        # calculates the probability of x for 1-dim Gaussian with mean mu and var. sigma
        return exp(- ((mu - x) ** 2) / (sigma ** 2) / 2.0) / sqrt(2.0 * pi * (sigma ** 2))


    def measurement_prob(self, measurement):

        # calculates how likely a measurement should be

        prob = 1.0;
        for i in range(len(landmarks)):
            dist = sqrt((self.x - landmarks[i][0]) ** 2 + (self.y - landmarks[i][1]) ** 2)
            prob *= self.Gaussian(dist, self.sense_noise, measurement[i])
        return prob

    def __repr__(self):
        return '[x=%.6s y=%.6s orient=%.6s]' % (str(self.x), str(self.y), str(self.orientation))


#myrobot = robot()
#myrobot.set_noise(5.0, 0.1, 5.0)
#myrobot.set(30.0, 50.0, pi/2)
#myrobot = myrobot.move(-pi/2, 15.0)
#print myrobot.sense()
#myrobot = myrobot.move(-pi/2, 10.0)
#print myrobot.sense()

myrobot = robot()
myrobot = myrobot.move(0.1, 5.0)
Z = myrobot.sense()

N = 1000
p = []
for i in range(N):
    x = robot()
    x.set_noise(0.05, 0.05, 5.0)
    p.append(x)

p2 = []
for i in range(N):
    p2.append(p[i].move(0.1, 5.0))
p = p2

w = []
for i in range(N):
    w.append(p[i].measurement_prob(Z))

p3 = []

추가되는 코드는 다음과 같습니다.

p3 = []
for i in range(N):
    weight_sum = 0
    rate = random.random()
    for particle, weight in zip(p2, a):
        weight_sum += weight
        if rate < weight_sum:
            p3.append(particle)
            break

이런 식의 비교는 비효율적입니다.

Resampling Wheel

이를 방지하기 위한 간단한 트릭이 있습니다. 모든 파티클 가중치가 하나의 원을 이룬다고 가정해봅시다. 각 가중치의 비중에 따라 섹션을 나눕니다.

파티클의 인덱스는 uniform한 확률로 결정된다고 정의합니다. 초기 베타 값은 0으로 설정합니다.

index = U[1...N]
b = 0

이제 b 업데이트를 N번 반복합니다. b에 더할 값도 0 ~ 2 * w_max 사이에서 랜덤 값을 구해줍니다. 위 그림에서 최대 가중치는 w5이며, b는 다음과 같이 변경됩니다.

이제 b가 해당하는 가중치를 찾아갑니다.

p3 = []
beta = 0
max_w = 2 * max(w)
index = random.randint(0, N)

for i in range(N):
    beta += random.uniform(0, max_w)
    while w[index] < beta:
        beta -= w[index]
        index = (index + 1) % N

    p3.append(p2[index])

p = p3
print p

Quiz

로봇의 오리엔테이션은 파티클 필터에서 영향을 미치지 않는다! 사실일까요?

정답은 No, 로봇의 오리엔테이션은 중요한 역할을 합니다.

로봇이 향한 방향이 달라지면, 이동 후 측정 과정에서 차이가 상당한 게 보이시나요?

파티클의 오리엔테이션이 로봇 오리엔테이션과 다르면 가중치가 작아지고, 파티클 생성을 반복하면 대부분의 파티클이 한 방향을 바라보게 만들 수 있습니다.

def eval(r, p):
    sum = 0.0
    for i in range(len(p)): # calculate mean error
        dx = (p[i].x - r.x + (world_size/2.0)) % world_size - (world_size/2.0)
        dy = (p[i].y - r.y + (world_size/2.0)) % world_size - (world_size/2.0)
        err = sqrt(dx * dx + dy * dy)
        sum += err
    return sum / float(len(p))

주어진 코드 eval(r, p)를 사용하여 로봇과 파티클 간의 유클리드 거리의 평균(= error)을 구해봅시다.

    # ...
    p = p3
    print eval(myrobot, p)

파티클을 초기 생성했을 때의 에러와 비교해보면 더 명확한 결과를 얻을 수 있습니다.

Filters

로봇의 위치 추정 과정에는 두 가지 업데이트가 있습니다. 측정 업데이트와 이동 업데이트가 그것입니다.

측정 업데이트는 사후 확률을 계산하는 과정입니다. 이는 베이즈 정리에 의해 likelihood * 사전 확률 값에 비례합니다.

이동 업데이트는 컨볼루션의 과정으로, 모든 변환 확률 * 사전 확률의 합입니다.

파티클 필터에서 이는 다음과 같이 나타납니다.