Tracking Methods
로봇의 위치를 추정하는 방법은 크게 세 가지로 나뉩니다.
| Monte Carlo | Kalman Filter | Particle Filter |
|---|---|---|
| discrete | continuous | continuous |
| multimodal | unimodal | multimodal |
Monte Carlo 방식은 지도를 셀로 나누고, 각 셀이 특정한 확률을 갖는 discrete 구조입니다. 또한 확률 분포가 일관되게 증가하다 감소하지 않기 때문에 multimodal 형태입니다.
Kalman Filter 방식은 가우시안 분포를 이용하며 위치를 추정함과 동시에 가속도 값을 예측할 수 있어 자주 사용되는 방식입니다. 가우시안 분포는 다음과 같이 연속적(continuous)이고, 단봉적(unimodal)으로 생겼습니다.
이후 강의에서 다룰 Particle Filter는 연속적이며 다봉분포를 가집니다.
more about Kalman Filter

가우시안 분포가 대칭이 되는 지점이 가우시안 분포의 평균이며, 앞으로 mu(= μ)라고 표현하겠습니다. 또한, 가우시안 분포는 분산이 작을수록 그래프가 높고 좁으며, 분산이 클수록 넓고 낮게 표현됩니다. 분산은 sigma2(= σ2)로 표현하겠습니다.
가우시안 분포 함수는 다음과 같이 표현합니다.
가우시안 분포의 분산이 클수록(= 폭이 넓을수록) 추정은 불확실하며, 분산이 작을수록(= 폭이 좁을수록) 확실합니다.
example
평균이 10, 분산이 4인 가우시안 분포 f(x)에서, x=8일 때 값을 구해봅시다.
f(x)를 파이썬 코드로 구현하면 다음과 같습니다.
# code
from math import pi, exp, sqrt
def f(mu, sigma2, x):
return exp(-0.5 * (x-mu)**2 / sigma2) / sqrt(2.0 * pi * sigma2)# output
>>> f(10, 4, 8)
0.12098536225957168가우시안 분포는 그 정의에 의해 x = mu일 때 값이 최대가 되며, 그때 값은 1 / sqrt(2 * pi * sigma2)가 됩니다.
review
로봇의 위치 추정 각 과정의 특징은 다음과 같습니다.
| \ | convolution | product | Bayes Rule | Total Probability |
|---|---|---|---|---|
| 측정(= measurement) | 0 | 0 | ||
| 이동(= motion) | 0 | 0 |
측정은 기저 확률을 업데이트(후 정규화)하며, 이동은 로봇이 어디로 이동했는지 파악하여 확률을 이동시킵니다. 이때 p(Z)를 계산할 때 사용했던 전체 확률 법칙이 사용됩니다.
measure and predict in Kalman Filter
measurement
칼만 필터에서도 역시 베이즈 정리를 이용한 측정과 전체 확률 법칙을 이용한 예측이 반복됩니다. 가우시안 분포를 베이즈 정리를 통해 계산해봅시다. 사전분포의 평균과 분산을 각각 mean1, var1, 측정값의 평균과 분산을 mean2, var2라 할 때, 사후확률의 평균 new_mean과 분산 new_variance는 다음과 같습니다.
def update(mean1, var1, mean2, var2):
new_mean = float(mean1 * var2 + mean2 * var1) / (var1 + var2)
new_variance = 1. / (1. / var1 + 1. / var2)
# same as
# new_variance = var1 * var2 / float(var1 + var2)
return new_mean, new_variance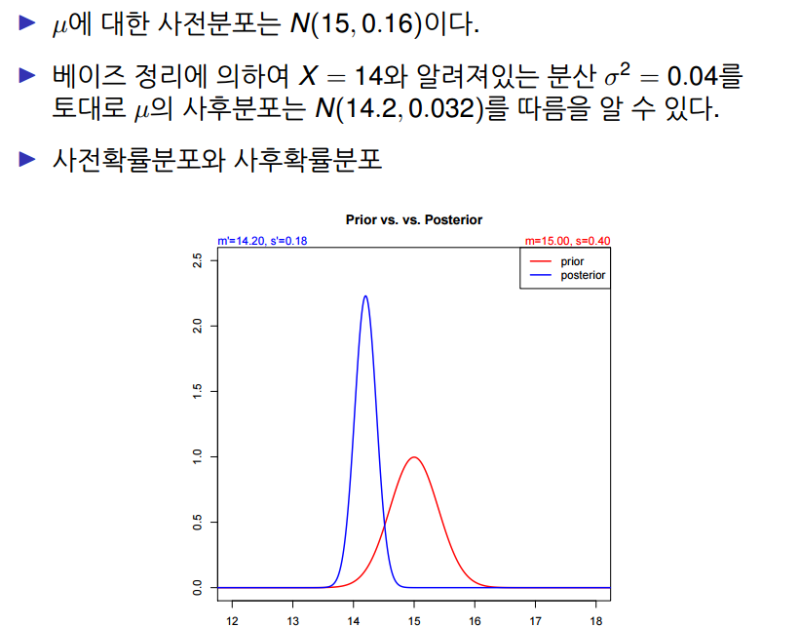
이때 새로운 평균은 이전 평균의 사이에 있으며, 분산이 더 작은 쪽에 가깝습니다. 분산은 항상 작아집니다.
motion
가우시안 분포의 이동을 표현하려면, 평균에 이동량을 더해줍니다. 로봇 하드웨어의 한계를 표현하기 위한 분산을 더해 불확실성을 증가시킵니다.
def motion(mean1, var1, mean2, var2):
new_mean = mean1 + mean2
new_variance = var1 + var2
return new_mean, new_variance오늘은 가우시안 분포를 사용하는 로봇의 예측과 이동에 대해 알아보았습니다. 다음 시간에는 칼만 필터를 사용하면 어떻게 속도를 측정할 수 있는지에 대해 알아보도록 하겠습니다.
'Robotics' 카테고리의 다른 글
| 40일차 - Update Kalman Filter (0) | 2020.08.12 |
|---|---|
| 39일차 - 2차원 Kalman Filter, Position과 Velocity의 상관관계 (0) | 2020.08.12 |
| 37일차 - 2D Localization (0) | 2020.08.06 |
| 36일차 - 조건부확률, 베이즈 정리, 1D Localization (0) | 2020.08.06 |
| 35일차 - ROS에서 dynamixel_sdk include 하기 (0) | 2020.08.05 |


