본문 바로가기
대학 수업

[응용수학II] Direction Field & Separable ODEs

엥휴 2020. 9. 7. 22:50
반응형

Direction Field

방향장이란 미분방정식의 기하학적 해석으로, 미분과 관계식을 가지고 있는 함수의 (x, y) 평면 상 특정한 점에서의 순간 기울기(순간 변화율)를 나타낸 그림입니다.

주어진 선분의 길이는 중요치 않으며, 다만 이 정도의 기울기 값을 가진다는 의미입니다. 찾는 함수가 (0, 0)을 지나는데, 육안으로는 기울기 값이 -1 정도 되어보이네요.

y'=f(x, y)의 1계 DE이며, explicit 하게 표현되어 있으면 기울기가 잘 드러납니다.

  • y' = x^2 + y^2 - 1, y(0) = 0
  • (1, 1) -> y' = 1
  • (2, 0) -> y' = 3

즉, 좌표평면 상의 찾으려는 함수가 지나게 되는 특정한 점에서의 기울기 값을 그래픽으로 그려놓은 것을 방향장이라고 할 수 있습니다.

빨간색 곡선은 integral curve라고 하며, 초기값 (0, 0)을 지나면서 주어진 Direction Field와 어우러지는 적당한 곡선을 의미합니다. 방향장 내에서 하나의 Integral Curve를 찾을 수 있습니다.

  • 초기값 문제
  • 일계 미분방정식
  • y' = f(x, y)

해당 사항을 만족하는 미분방정식은 Direction Field로 함수를 찾아낼 수 있습니다. 이는 일변수함수의 선형 근사식을 이용한 사항입니다.

y' = f(x, y), y(x_0) = y_0인 미분방정식의 순간 기울기가 알려져있다고 합시다. x_0, y_0의 슬로프는 f(x_0, y_0)일 때, x가 delta x만큼 증가하면 y는 y(x_0 + delta x) = y_0 + f(x_0, y_0) * delta x가 됩니다. 이를 순차적으로 반복하면 모든 순간 기울기를 나타내는 함수 값을 찾을 수 있으며 이를 오일러 방법이라고 합니다.

y' = x^2, y(0) = c인 상황을 생각해봅시다. 단순히 적분을 사용하여 해결해보면 y = 1/3 x^3 + c라는 함수가 나옵니다. 방향장에서 이를 확인해볼까요?

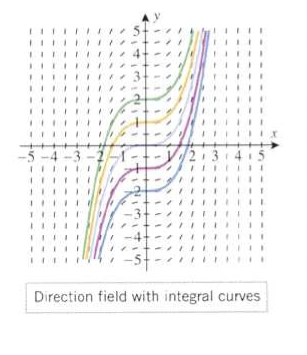
c의 위치에 따라 다양한 integral curve가 생기는 것을 확인할 수 있습니다.

y' = - x / y, y(1) = 1의 그래프는 어떨까요? 도함수의 형태에 따라 다음과 같은 식이 성립하는 걸 알 수 있습니다.

  • x = y -> y' = -1
  • x = -y -> y' = 1
  • x = 0 -> y' = 0
  • y = 0에 가까워질수록 -> y' = +- 무한대
  • (0, 0)일 때는 결정할 수 없음

따라서 (1, 1)을 따르는 둥근 원형을 따르게 됩니다. y'을 적분해보면,

\int y\cdot dy=\int -x\cdot dxy^2+x^2=cy^2+x^2=2

Separable ODEs

Separable ODE는 양쪽 항을 각각 y 적분, x 적분할 수 있도록 이항할 수 있는 형태를 말합니다. 그러나 모든 미분방정식이 그렇게 되는 건 아닙니다.

1. 9yy' + 4x = 0

9yy' + 4x = 09y\frac{dy}{dx}=-4x\int9y\cdot{dy}=\int-4x\cdot{dx}\frac92y^2=-2x^2+c\therefore4x^2+9y^2=c

2. y' = 1 + y^2

\frac{dy}{dx}=1+y^2\Rightarrow\frac{1}{1+y^2}dy=dx\Rightarrow\int\frac1{1+y^2}dy=\int{dx}\Rightarrow\tan^{-1}(y)=x+c\therefore{y=\tan(x+c)}

3. y' = ky

\frac{dy}{dx}=ky\Rightarrow\int\frac{dy}{y}=k\cdot{dx}\Rightarrow\ln{|y|}=kx+c\Rightarrow|y|=e^{kx}*e^c\therefore{y}=c\cdot{e}^{kx}

4. y' = - y / x

\frac{dy}{dx}=-\frac{y}{x}\Rightarrow\frac{dy}{y}=-\frac{dx}{x}\Rightarrow\int\frac{dy}{y}=\int-\frac{dx}{x}\Rightarrow\ln|y|=-\ln|x|+c\therefore\ln|xy|=c

5. 2xyy' = y^2 - x^2

변수 분리형은 아니지만 separable 취급할 수 있는 꼴입니다. y'=f(y/x) 꼴일 때, y/x를 u로 치환하여 도함수를 separable 한 형태로 만들고, x와 u에 관한 y'을 만들면 separable form으로 만들 수 있습니다. 이 과정을 reduction to separable form이라 합니다.

2y'=\frac{y}{x}-\frac{x}{y}u=\frac{y}{x},\,y=xu\Rightarrow{y'}=u+xu'=\frac{1}{2}\(u-1/u\)\Rightarrow\int\frac{-2u}{u^2+1}du=\int\frac1x\cdot{dx}\therefore-\ln|u^2+1|=\ln|x|+c,\,\ln|x(u^2+1)|=c\therefore\ln|\frac{y^2}{x}+x|=c,\,|\frac{y^2}{x}+x|=e^c,\,\frac{y^2}{x}+x=c

잠깐! x / (x^2+1) 꼴의 적분 설명

\int\frac{x}{x^2+1}dx=\frac12\ln|x^2+1|+cu=x^2+1,\,du=2x\cdot{dx},\,x\cdot{dx}=\frac12du\int\frac{\frac12du}{u}=\frac12\ln|u|+c=\frac12\ln|x^2+1|+c

6. (2x - 4y + 5)y' + (x - 2y + 3) = 0

u=x-2y, y'=\frac{1-u'}2\(2u+5\)y'=-u-3=\(2u+5\)\(\frac{1-u'}2\)\Rightarrow\(2u+5\)u'=4u+11\Rightarrow\int\frac{4u+10}{4u+11}du=\int\(1-\frac1{4u+11}\)du=\int{2dx}\Rightarrow{u}-\frac14\int\frac4{4u+11}du=2x+c\Rightarrow4u-\ln|4u+11|=8x+c\therefore4x+8y+\ln|4x-8y+11|=c

반응형
저작자표시 비영리 변경금지

'대학 수업' 카테고리의 다른 글

[동역학] Curvilinear Motion(곡선 운동), Projectile Motion(포물선 운동)  (0) 2020.09.08
[임베디드컴퓨터구조] 임베디드 컴퓨터의 정의, 특징, 평가 기준  (0) 2020.09.07
[동역학] 직선 운동과 곡선 운동  (0) 2020.09.03
[응용수학II] Ordinary(Particular) Differentiation Equations  (0) 2020.09.02
[동역학] Kinematics of a Particle  (0) 2020.09.01

'대학 수업' Related Articles

엥왜안됨초보 프로그래머 블로그 하루의 시작은 엥?? 왜 안 되지.. 하루의 끝은 휴~~해결했다

티스토리툴바